Übungsaufgaben Robotik

A1 - A2 - A3 - A4 - A5 - A6

Allgemeines

Im Unterverzeichnis vorgaben stehen Programme, die von uns vorgegeben werden. Die Dateien können in ein eigenes Verzeichnis kopiert und übersetzt werden.

In adair bzw. roblib befinden sich die zur Verfügung gestellten Pakete. Diese sind schon übersetzt und können verwendet werden.

In den einzelnen Aufgabenstellungen steht, welche Pakete für welche Aufgaben gedacht sind.

Die Aufgaben bestehen im wesentlichen aus Implementierungsarbeiten. Demzufolge ist für die Abnahme der Aufgaben die Funktionsfähigkeit der erstellten Software am jeweiligen Rechnertermin vorzuführen. Dafür sind, sofern nicht explizit angegeben, geeignete Testszenarien zu entwerfen, die alle geforderten Fähigkeiten der Programme demonstrieren. Sollten in den Aufgaben zusätzliche theoretische Fragen gestellt sein, so sind die Lösungen ebenfalls zu diesem Termin zu übergeben. Die auf der semesterspezifischen Seite genannten Abgabetermine sind verbindlich.

Für die Aufgaben 1 bis 3 werden die roten Roboter vom Typ RM-501 und für Aufgabe 4 bis 6 werden die grauen Roboter vom Typ RV-M1 im Raum EN266a verwendet.

Während der Programmausführung muß der Notausschalter immer in Reichweite sein und der Roboter beobachtet werden, um ggf. sofort abschalten zu können.

Nützliche Programme:

init

Initialisieren der Ada-Umgebung.

Aufruf in der Shell, in der die Ada-Umgebung benutzt werden soll.

Die Befehle können natürlich auch in .cshrc/.bashrc aufgenommen werden. (SOLLTE DER AUFRUF "source ~pdv/lehre/robotik/init" MIT EINER FEHLERMELDUNG ENDEN, KÖNNTE ES DARAN LIEGEN, DASS ER NICHT IN DER RICHTIGEN SHELL GESTARTET WURDE. JE NACH VERWENDETER SHELL GIBT ES init.tcsh UND init.bash. STANDARD IST init == init.bash!)

Bitte überprüfen Sie, ob Sie noch alte Einstellungen aus Eingebettete Echtzeitsysteme z.B. in der Datei .cshrc oder .bashrc haben, und löschen Sie diese zuerst! Die Umgebung für Robotik ist verschieden.

makelib

Erzeugen einer Ada-Library. Aufruf in dem Verzeichnis, aus dem eine Ada-Library gemacht werden soll. Es werden mehrere notwendige Dateien und Unterverzeichnisse angelegt.

Achtung: makelib funktioniert nur auf dem Rechner pueblo. Also: auf pueblo einloggen ($ ssh pueblo), makelib aufrufen, ausloggen.

start

Syntax: start RECHNERNAME EXECUTABLE

Lädt ein Vorprogramm zur Identifikation auf den Zielrechner und nach Bestätigung das Benutzerprogramm. Die Zielrechner heissen "blei", "platin" und "silber" und stehen im Raum EN266a. Daran angeschlossen sind entweder die roten Roboter RM-501 oder die grauen Roboter RV-M1 zur Benutzung mit AdaIR.

Beispiel:

1. Initialisieren der Ada-Umgebung:
$ source ~pdv/lehre/robotik/init
2. Erzeugen einer Ada-Library:
$ mkdir a1
$ cd a1
$ ssh pueblo
$ cd a1
$ makelib
$ exit
Die Datei ada.lib enthält alle Verweise auf andere Ada-Libraries, die Pakete zur Verfügung stellen (z.B. auf ~pdv/lehre/robotik/roblib).
3. Eingabe eines Programms mit einem Text-Editor (z.B. vi, emacs) mit dem Datei-Namen hello.ada:
with TEXT_IO; use TEXT_IO;
procedure hello is
begin
  put ("Hello, world.");
  new_line;
end hello;
Übersetzen:
$ ada hello.ada
4. Binden:
$ a.ld hello -o hello.vox
(erzeugt ausführbares Programm hello.vox; Hauptprogramm ist procedure hello)
5. Ausführen auf dem Zielrechner:
$ start blei hello.vox

Allgemeine Hinweise

• Weder Compiler noch Linker sind zimperlich oder gar fehlerfrei. Deshalb gelten folgende goldene Regeln:
• Immer mit -O0 (keine Optimierung) übersetzen.
• Nie INLINE-Code verwenden - der wird auch bei -O0 optimiert.
• Zugriffe auf Register, Abwarten einer Zeitspanne oder ähnliche Dinge werden vom Compiler/Linker häufig als völlig unnütz betrachtet und wegoptimiert. Das kann das Laufzeitverhalten erheblich beeinflussen. Wird eine Prozedur (aber nicht ihr Aufruf) beim Linken entfernt, führt ihr Aufruf notwendigerweise zum Programmabsturz.
• Ein-/Ausgabe auf den Echtzeitrechnern über Port 3 geschieht automatisch ohne Angabe des Parameters:
with serial_io;
serial_io.PutS("Hello, world!");
• Ein-/Ausgabe auf den Suns erfolgt über TEXT_IO.
• Bei hängendem Programm erst "Abort" und dann "Reset" drücken, damit das xterm wieder benutzbar wird.
• Achten Sie bitte bei der Benutzung der roten Roboter auf korrektes Nesten der Hand. Das Neigegelenk muß anhalten sobald der Taster klickt. Sollten Sie dennoch ein Nachlaufen beobachten, so schalten Sie ihn sofort per Not-Aus aus und benutzen diesen Roboter bitte nicht mehr für eine Weile. Dieser Fehler liegt möglicherweise in der Leistungselektronik des Steuergerätes begründet,  ist leider kaum reproduzierbar und somit schwer zu beheben. Er erzeugt wahrscheinlich Motorausfälle, die zu Kosten von jeweils mindestens 125 Euro und einer Stunde Arbeit führen.
• Beachten Sie bei der Benutzung der weissen Roboter darauf, dass der NOT-AUS-Taster gelöst ist. Ggf.  muss danach am Steuergerät der Reset-Knopf gedrückt werden.
• Bei start->SCHEISS_SEMAPHORE ist möglicherweise das Terminal schuld. In der oberen Statuszeile steht dann z.B. "HOLD". Dieser Zustand kann mit F1 verlassen werden. Das Terminal könnte auch OFF-LINE sein. Im Config-Menü(F3->F7->Online/local) kann man dann auf ON-LINE umschalten.
• Das unmittelbare Echo des Terminals kann manchmal ausfallen. Entweder man denke sich die Ausgabe der eigenen Eingaben oder stellt die entsprechende Einstellung im Config-Menü(F3) um.
• Verwendung generischer Pakete: Wenn ein generisches Paket (z.B. TBOX) verwendet werden soll, so darf nur eine neue Instanz gleichen Namens erzeugt und verwendet werden. Der Compiler wird sonst verwirrt und äußert sich entsprechend, was nicht gerade hilfreich ist. Es treten Fehlermeldungen wie "Typ der Prozeduraufrufparameter stimmt nicht mit früherer Definition überein!" auf. Soll also TBOX z.B. für die Hauptprozedur und das lokale Paket "modul" verwendet werden, bietet sich folgende Vorgehensweise an:

      -------------------------
      -- modul_s.ada:
      with TBox;
      package MyTBox is new TBox("Titeltext");
      with MyTBox; use MyTBox;
      with ...;    use ...;
      package modul is
        ...
      end modul;
Natürlich muß "with TBox; package MyTBox is new TBox("Titeltext");" vor dem Mudulimport für "modul" stehen, da das eine Paketdefinition ist und somit sozusagen den Modulimport für "MyTBox" abschließt.
      -------------------------
      -- modul_b.ada:
      with MyTBox; use MyTBox;
      with ...;    use ...;
      package body modul is
        ...
      end modul;
      -------------------------
      -- main_b.ada:
      with MyTBox; use MyTBox;
      with ...;    use ...;
      procedure main is
        ...
      end main;
Das Paket MyTBox ist in modul_s.ada definiert. Obwohl nur eine Datei übersetzt werden muß, werden der lokalen Ada-Library zwei Pakete hinzugefügt. Es gibt in Ada also keinen zwingenden Zusammenhang zwischen Datei- und Modulstruktur!

Einige Hinweise zum Umgang mit AdaIR und den Echtzeitrechnern

• Korrektur im AdaIR-Handbuch: Statt DefineBase muß es SetBase heißen. (z.B. in der Beschreibung der Prozedur MoveFrameRelative)
• Hin und wieder scheint sich der Rechner während einer Bewegung mittels der AdaIR-TeachBox aufzuhängen. Das Problem ist bekannt und scheint an silber öfter als an blei aufzutreten. Bisher konnte aber keine Lösung gefunden werden, da der Fehler nicht zuverlässig zu reproduzieren ist und vermutlich in der Terminal-Rechner-Verbindung begründet ist. Dann hilft nur noch: Drücken von ABORT gefolgt von RESET am Echtzeitrechner.
• Für die Steuerung mittels AdaIR sind grundsätzlich die Roboter vom Typ RV-M1 zu benutzen (weisse Roboter).
• Beispielprogramm ellipse.ada in den Vorgaben:

Übersetzen mit
    ada ellipse.ada
Binden mit
    a.ld -o ellipse.vox ellipse
Ausführen z.B. mit
    start platin ellipse.vox

Aufgabe 1: Sanfte Winkelbewegung

Aufgabenstellung

Wenn ein Gelenk an den Sollwinkel 0 gefahren wird und am Ende keine Endabschalterberührung vorliegt, muß für das entsprechende Gelenk eine Nest-Bewegung ausgeführt werden.
Wenn während der Bewegung auf den Endabschalter zu der Endabschalter des Gelenks betätigt wird, muß die Bewegung sofort abgebrochen und die entsprechende Komponente des Vektors IST_POSITION auf 0 gesetzt werden.
Darüber hinaus soll für das in den Endabschalter gefahrene Gelenk eine Nest-Bewegung ausgeführt werden, falls die Schalterberührung früher als nach der IST_POSITION zu erwarten erfolgte.

Zur sinnvollen Auswertung der Endabschalterzustände und Benutzung der Nest-Prozedur soll eine Schalterhysterese (siehe EES) verwendet werden.
In einer speziellen 0-Umgebungen (Interval um 0) muß geeignet zwischen Halt und Nest  unterschieden werden. Die gewählte Lösung ist zu begründen.

Die Drehrichtung der Gelenke darf nicht geändert werden, um Verwirrungen zu vermeiden.

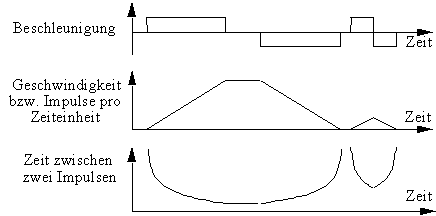
Zur Verhinderung von abrupten Bewegungsänderungen muß die vorgegebene Prozedur GELENKSCHRITT so aufgerufen werden, daß ein Auftrag zuerst mit von 0 konstant steigender Geschwindigkeit (a geeignet wählen!), dann mit maximaler Geschwindigkeit (geeignet wählen!) und zum Schluß mit konstant bis auf 0 sinkender Geschwindigkeit abgearbeitet wird (Rampenfunktion). Bei kürzeren Bewegungen fällt die mittlere Bewegungsphase weg, und die Rampen sind gegenüber dem Normalfall entsprechend verkürzt. Wesentliche Größen dieses Bewegungsablaufs sind die Zeit t, die aktuelle Gelenkgeschwindigkeit v, die beim Beschleunigen und Bremsen jeweils konstante Beschleunigung a und die Schrittnummer bzw. Strecke s. Zum Verzögern des Programms bzw. Roboters gibt es zwei Möglichkeiten:

1. Man führt for..to-Schleifen zur Verzögerung pro Schritt durch. Dazu müssen Sie die Funktion 1/v(s) herleiten und benutzen.
2. Man fragt die Systemzeit mittels CLOCK aus dem Paket CALENDAR ab und berechnet aus der aktuellen Zeit, bis zu welchem Schritt die Bewegung jeweils ausgeführt sein muß. Dazu müssen Sie die Funktion s(t) herleiten und benutzen. Vorsicht: Die Anzahl der "mit einmal" ausführbaren Gelenkschritte ist auf 10 zu beschränken!

Bitte beachten Sie, daß eine konstante Beschleunigung nicht durch eine lineare Änderung der Wartezeit bzw. durchlaufenen Schleifenzahl erreicht wird (siehe Bild):

Schreiben Sie ein Programm, das unter Verwendung der neuen Prozedur GELENKBEWEGUNG einzelne Gelenke in am Terminal eingebbare Winkel  UND Gelenkschrittnummern bewegen kann. Ihr Programm muß außerdem gewährleisten, daß die mechanischen Grenzen der einzelnen Gelenke (siehe gelenke_s.ada) nicht überschritten werden (Bewegungsbeschränkung im Schritte-Bereich!); entsprechende Benutzereingaben sind zurückzuweisen. Das Programm soll mit einem Tastendruck terminiert werden können.

Hinweise

Wenn das Handneigegelenk aus seiner "Null-Position" herausgefahren ist, wird der Endabschalter des Handdrehgelenks nicht mehr betätigt. D. h., der Endabschalter EA4 kann nur betätigt werden, wenn der Endabschalter EA3 betätigt ist.

Aufgabe 2: Gelenkinterpolierte Bewegungen und Teachbox

Aufgabenstellung

Implementieren Sie eine Teachbox, mit der durch einzelnen Tastendruck Gelenke mit kleiner Schrittweite in positiver oder negativer Drehrichtung bewegt werden können. Während die Taste gedrückt ist, soll die Bewegung nicht stoppen. Sobald die Taste losgelassen wird, muß die Bewegung schnellstmöglich aufhören. Über die Tastatur soll die Hand durch einen Tastendruck geöffnet bzw. geschlossen und die Prozedur NEST ausgeführt werden können. Weiterhin sollen die aktuelle Position und der derzeitige Handzustand unter einer Nummer abgespeichert werden können. Mindestens 10 gespeicherte Positionen sollen anschließend als geteachtes »Programm« automatisch hintereinander angefahren werden können.

Geben Sie mit Hilfe der implementierten Teachbox ein Programm ein, das einen auf dem Tisch liegenden Würfel an einer anderen Position auf dem Tisch ablegt.

Hinweise

  procedure TeachBox (Kommando : out T_TbKommando;
                      Geschw   : out T_Geschwindigkeit);

Um eine kontinuierliche und möglichst ruckfreie Bewegung zu erreichen, müssen mehrere Gelenkschritte pro Tastenabfrage ausgeführt werden. Probieren Sie aus, wie viele für das Programm am günstigsten sind.

Es ist wahrscheinlich hilfreich, GELENKBEWEGUNG in eine Task umzuwandeln, die die Bewegungsdienste per Entry bereitstellt. Dies erlaubt eine Parallelisierung mit der Ansteuerung der Hand, die am besten ebenfalls aus einer eigenen Task heraus realisiert wird.

Bedenken Sie, daß Task-Wechsel nur stattfinden, wenn eine Task blockiert wird oder eine DELAY-Anweisung ausführt. Ggf. müssen Sie DELAY 0.0 verwenden, um Task-Wechsel zu erzwingen.

Aufgabe 3: Rückwärtsrechnung, Orientierungsanpassung und achsenparallele Bewegungen

Aufgabenstellung

Zur Implementierung des xyz-Modus ist sowohl eine Vorwärtsrechnung wie auch eine Rückwärtsrechnung erforderlich. Die Vorgehensweise wird anhand des Fahrens entlang der z-Achse beschrieben: Der Roboter befindet sich in einer beliebigen Stellung und soll bei gleichbleibender Orientierung um 10.0 mm entlang der z-Achse des BKS bewegt werden. Mit Hilfe der Vorwärtsrechnung wird aus den aktuellen Gelenkwinkeln eine homogene 4x4-Matrix bestimmt. Bewegen entlang der z-Achse bedeutet, auf das Element (3,4) (der z-Komponente des Positionsvektors) den Verfahrweg (Dz = 10.0 mm) zu addieren. Aus dieser neuen Matrix sind mit Hilfe der Rückwärtsrechnung die neuen Gelenkwinkel zu bestimmen und gelenkinterpoliert anzufahren.

Das Vorgehen beim Bewegen entlang der x- bzw. y-Achse ist ähnlich. Allerdings muß dabei berücksichtigt werden, daß aufgrund der globalen Degeneration des RM501 eine Orientierungsanpassung erforderlich ist. D. h., es sind nicht alle Positionen mit einer beliebigen Orientierung anfahrbar. Um festzustellen, ob eine gegebene Stellung W in Form einer homogenen Matrix anfahrbar ist, muß folgende Bedingung (Degenerationsbedingung) gelten:

W (2,3) * W (1,4) = W (1,3) * W (2,4)

Die Rückwärtsrechnung akzeptiert nur Matrizen, bei denen diese Bedingung erfüllt ist (sonst wird die Ausnahme FRAMEINVALID ausgelöst). Bevor also die Rückwärtsrechnung aufgerufen werden kann, muß der Orientierungsteil der Matrix angepaßt werden, d. h., die vorgegebene Position ist mit einer möglichst geringen Orientierungsänderung anzufahren.

Lernen Sie mit Hilfe dieser veränderten Teachbox erneut ein Programm ein, das einen auf dem Tisch liegenden Würfel an einer anderen Position auf dem Tisch ablegt. Dafür sind jetzt allerdings vorrangig Bewegungen bezüglich des kartesischen Koordinatensystems zu verwenden.

Hinweise

Das vorgegebene Modul RM501_KINEMATIK stellt sowohl die Vorwärts- wie auch die Rückwärtsrechnung für den RM501 zur Verfügung. Dieses Modul exportiert folgende zwei Prozeduren:

VORWAERTSRECHNUNG - bestimmt aus vorgegebenen Gelenkwinkeln die homogene 4x4-Matrix

RUECKWAERTSRECHNUNG - berechnet aus einer homogenen 4x4-Matrix die Gelenkwinkel

beschreibt eine Stellung, in der der Roboter den Arm vollständig nach oben streckt. Dies entspricht einer Gelenkwinkeleinstellung von (150.0, -13.5, 90.0 , 90.0, 112.5) Grad. Die Rückwärtsrechnung liefert nur Gelenkwinkel, die innerhalb der Bewegungsmöglichkeiten der Gelenke liegen. D. h., eine theoretisch zwar mögliche Lösung für das erste Gelenk von -90.0° wird auf den Winkelbereich [0.0°...300.0°] des ersten Gelenkes angepaßt, das Ergebnis ist also 270.0°. Eine Untersuchung der Lösung ist nur dann erforderlich, wenn zwei Lösungen geliefert werden. Von diesen zwei Lösungen ist die plausibelste auszuwählen.

Das Paket ROBOTER_MATHE enthält einige kleine Prozeduren, die von RM501_KINEMATIK benutzt werden, beispielsweise ATAN2 und Funktionen zur Winkelkonvertierung.

Aufgabe 4: Bewegungsbahnen

Aufgabenstellung

Zur Steuerung des Roboters steht das Paket aufgabe4_vorgaben zur Verfügung. Dieses Paket stellt die grundlegenden Prozeduren, entsprechend den vorigen Aufgaben, für den RV-M1 bereit. Aus Effizienzgründen überprüfen die vorgegeben Prozeduren nicht, ob die Grenzgeschwindigkeiten für die einzelnen Gelenke eingehalten werden. Die per Tastatur eingebbare Zeitvorgabe für das Abfahren der gesamten Bahn ist deshalb groß genug (20 s) zu wählen.
Dem Beispielprogramm bahn.ada ist zu entnehmen, wie die Prozeduren verwendet werden können. Die darin enthaltenen Start- und Zielpunkte können als Beispiel zur schnellen Demonstration verwendet werden.

Es ist im Gelenkraum zu interpolieren!
Was passiert bei einer Bahninterpolation im kartesischen Raum?

Hinweise

Aufgabe 5: Bewegungsplanung mit Konfigurationshindernissen und A*

Aufgabenstellung

Schreiben Sie ein Programm, das z. B. mit Hilfe der Teachbox ein Start- und ein Zielpunkt innerhalb der Arena festlegen läßt. Dann soll eine kollisionsfreie Bewegungsbahn vom Start- zum Zielpunkt durch A*-Suche im Konfigurationsraum-Sichtbarkeitsgraphen geplant und anschließend ausgeführt werden. Ihr Programm soll mehrere Planungs- und Ausführungsvorgänge ohne Neustart erlauben. Beispielhafte Start/Zielpunkt-Kombinationen können zur schnellen Vorführung vorbereitet werden.

Die Arbeit bzw. der Erfolg der A*-Suche soll am Bildschirm dokumentiert werden. Damit soll nachvollzogen werden können, ob z.B. der Start- und/oder Zielpunkt in einem Hindernis liegt oder von anderen Punkten aus nicht gesehen werden kann. Ein "Nach-Teachen" des betreffenden Punktes soll damit möglich sein.

Die Beschreibung der Hindernisse in der Arena sowie eine Reihe von Hilfsroutinen sind im Paket HINDERNISSE (Datei hindernisse_s.ada) vorgegeben. Hindernisse sind dort stets aus achsenparallelen Quadern zusammengesetzt. Die Konstante ArenaO gibt den Ursprung der Arena im BKS wieder. In der HindernisListe ist das Hindernisgebirge zusammen mit 6 Quadern zur Arbeitsraumbegrenzung in BKS-Koordinaten enthalten.

Bevor Sie den Sichtbarkeitsgraphen berechnen, müssen Sie die Arbeitsraumhindernisse in Konfigurationsraumhindernisse überführen, indem Sie alle Quader geeignet vergrößern. Da das bewegte Objekt nur eine Drahtspitze ist, sind wenige Millimeter hierfür ausreichend (z.B. 5mm).

Die Knoten des Sichtbarkeitsgraphen sind bekanntlich Ecken der Konfigurationsraum-Hindernisse. Bei Ihrer Lösung sollen ausschließlich die vier oberen Ecken jedes Konfigurationsraum-Hindernisquaders als Knoten dienen, allerdings jeweils um eine feste Strecke dz nach unten verschoben, damit die Ecken der Höhe 5 nicht von der Arbeitsraumbegrenzung eliminiert werden. Wählen Sie dz passend zur Steingröße und der von Ihnen vorgenommenen Hindernisvergrößerung. Mit dieser Konvention enthält der Sichtbarkeitsgraph 4 Knoten pro Hindernisquader plus den Start- und den Zielpunkt, also 94 Knoten.

Hinweise

Die Arena ist nur dadurch vollständig für den Roboter erreichbar, daß die Handneigung in Abhängigkeit von der x-Koordinate variiert wird. Verwenden Sie die vorgegebene Funktion Arena2Frame, um für eine Arenaposition (x,y,z) eine erreichbare Roboterstellung einschließlich Orientierungsanpassung zu erhalten. Arena2Frame akzeptiert nur Positionen innerhalb der Arena, anderenfalls wird die Ausnahme E_OUT_OF_ARENA ausgelöst.

Leider ist der Arbeitsraum der Roboter ein wenig "verbogen". Soll z.B. ein Rechteck abgefahren werden, das aus entsprechend berechneten Punkten besteht, wird der TCP tatsächlich auf einem Trapez bewegt. Strecken, die "nah" am Roboter abgefahren werden, scheinen so z.B. in der Realität kürzer als theoretisch ebenso lange Strecken, die aber mit ausgestrecktem Arm vollzogen werden. Die entstehenden Differenzen sind aber klein und verschwinden nahezu vollständig in der Hindernissvergrößerung.

Die Positionen für Roboter und Arena sind auf dem Labortisch markiert. Es ist aber sinnvoll, am Anfang Ihres Programms einmal die gesamte Arena in Höhe des höchsten Hindernisses zu umfahren, um insbesondere die Orientierung und Position des Roboters hinreichend exakt (besonders im Hinblick auf die o.g. Arbeitsraumverbiegung) zu machen.

Um eine weitgehend lineare Bewegung zwischen den berechneten Stützpunkten zu erreichen, kann (muss aber nicht) statt der AdaIR-Prozedur auch die 4-3-4-Bahn aus Aufgabe 4 verwendet und die Annäherungs- und Abrückstellung in Arenapositionen linear interpoliert werden (nach 1/3 bzw. 2/3 jedes Wegstücks). Damit kommt der Roboter an den Knickpunkten jeweils zur Ruhe. Die hierbei noch auftretenden Abweichungen von einer vollständig linearen Bewegung können (hoffentlich) vernachlässigt werden - zumindest schließt der Versuchsaufbau Schäden aus.

Bei der parallelen Verwendung von aufgabe4_vorgaben und der AdaIR-Pakete, kann es zu Verwirrungen beim Kompilieren kommen. Durch explizite Angabe des Paketes, aus dem ein Bezeichner stammt oder stammen soll, wird das vermieden.

Aufgabe 6: Bewegungsplanung mit Potentialfeldern

Aufgabenstellung

Vor dem ersten Planungsvorgang soll Ihr Programm das Potentialfeld mit Hilfe der Funktion MaleFeld aus HINDERNISSE auf dem Terminal visualisieren. Hierbei ist aber auf die Ausrichtung der Achsen zu achten, so daß der Vergleich von Bildschirm und Realität einfacher wird. Dies erfolgt am besten auf Tastendruck nacheinander für jeweils eine Ebene in den Rasterhöhen 1, 2, 3, 4 und 5. Achten Sie auf eine geeignete Übersetzung der Potentialwerte in die darstellbaren Grauwerte vom Typ T_Grauwert.

Das Potential U(p) im Punkt p setzt sich aus einem anziehenden (negativen) Potential am Zielpunkt t und einer Überlagerung abstoßender (positiver) Potentiale an den Grenzflächen der Hindernisquader zusammen und berechnet sich so:

Dabei sind dist(p,i) der Abstand von p zum i-ten Hindernisquader und d_max eine obere Schranke für diese Entfernung, oberhalb der das jeweilige Hindernis keinen Beitrag mehr zum Potential liefert. d_max und die restlichen Parameter sind geeignet zu wählen. Für d_max  scheinen 5mm sinnvoll zu sein, damit Wege auch über Hindernisse der Höhe 4 gefunden werden können.
Zur Berechnung von dist(p,i) kann die vorgegebene Funktion QuaderAbstand benutzt werden. Sie berechnet den Abstand zwischen p und dem am nächsten liegenden Punkt des Hindernisquaders.
Für das konstante Verhältnis zwischen anziehendem und abstoßenden Potential empfiehlt sich 1/3000. Natürlich kann und soll experimentiert werden!

Die Bahnplanung soll als Gradientenabstieg erfolgen. Der Gradient G(p) im Punkt p gibt die Richtung der steilsten Potentialzunahme von p aus an. Für die Aufgabe soll eine numerische Näherung der Gradientenberechnung verwendet werden:

Da der Betrag von G(p) nicht benutzt werden soll, kann die Division durch Epsilon auch entfallen. Der jeweils nächste Bewegungsschritt erfolgt nun mit fester Schrittweite d_step entgegen der Richtung des Gradienten, da das Potential am Zielpunkt minimal sein sollte:

Sie brauchen kein Verfahren zur Vermeidung lokaler Minima zu implementieren. Wählen Sie einfach eine geeignete Maximalzahl von Iterationsschritten passend zu d_step. Die Bahnplanung terminiert, wenn der Zielpunkt hinreichend gut erreicht ist.

Der Roboter soll sich gleich während der Planung mitbewegen, da der Gradientenabstieg ein lokales Verfahren (greedy) ist.

Hinweise

Zum Fahren der Bahn sollten Sie eine langsame Geschwindigkeit wählen.

Bei dieser Aufgabe ist es sinnvoll, wiederum die Bahnberechnung aus Aufgabe 4 zu verwenden. Diesmal können die Stützpunkte jedoch in der Folge Start-, Abrück-, Annäherungs- und Zielposition verwendet werden, wobei die Zielposition jeweils der Startposition des nächsten Bewegungssegments entspricht. Sie erhalten somit für je drei Stützpunkte ein neues Bahnsegment, und der Bewegungsablauf stoppt nur an jedem dritten Stützpunkt.

Letzte Änderung 4.3.2003 von Mathias Neumann
Prozeßdatenverarbeitung