Lernziele
- Stochastische Modellierung und Leistungsbewertung
- Optimierung
Unterlagen
- Vorlesungsunterlagen zu Petri-Netzen
- TimeNET User Manual Version 3, Version 4
- gnuplot-Dokumentation
- Modell aus Aufgabe 2
- Messwerte aus Aufgabe 1
Aufgabenstellung
Teil 1 - Manuelle Lösung von GSPN
Gegeben sei das folgende GSPN-Modell einer Bearbeitungsstation mit Ausfall und Reparatur.
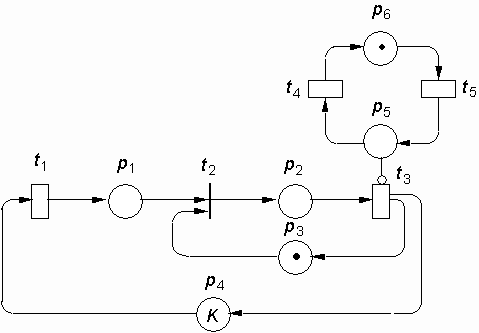
Die Bedeutung und die mittlere Schaltzeit der einzelnen Transitionen kann der folgenden Tabelle entnommen werden.
| Transition | Bedeutung | mittlere Schaltzeit |
|---|---|---|
| t1 | Transport eines Werkstücks zur Bearbeitungsstation (single server) | 1 |
| t2 | Beginn der Bearbeitung | - |
| t3 | Bearbeitung | 1 |
| t4 | Reparatur der Bearbeitungsstation | 1 |
| t5 | Ausfall der Bearbeitungsstation | 10 |
Es soll die stationäre Analyse manuell für K = 2 durchgeführt werden:
- Erzeugen Sie den vollständigen und den reduzierten Erreichbarkeitsgraph. Geben Sie eine Numerierung der andauernden Zustände an.
- Ermitteln Sie die zugrundeliegende Markow-Kette, geben Sie den Zustandsgraph und die Generatormatrix an.
- Ermitteln Sie die stationäre Lösung. Stellen Sie dazu das zugehörige lineare Gleichungssystem auf und lösen es.
- Ermitteln Sie den Durchsatz. Der Durchsatz ist definiert als die mittlere Schaltfrequenz der Transition T1 bzw. T3.
Teil 2 - Modellbasierte Optimierung der Zuggeschwindigkeiten
Für die spätere Eisenbahnsteuerung soll nun das Verhältnis der Lokgeschwindigkeiten so berechnet werden, dass die Summe der Lok-Wartezeiten möglichst gering wird.
Passen Sie dazu die Schaltzeiten der zeitbehafteten Transitionen Ihres Zugmodells aus Aufgabe 2 so an, dass sie den in Aufgabe 1 gemessenen tatsächlichen Gegebenheiten entsprechen. Tragen Sie die (relativen bzw. normierten) Fahrtzeiten von Zug 2 fest ein, für Zug 1 dagegen multipliziert mit einem Faktor g. Dieser Faktor wird als Parameter im Modell definiert und erlaubt die einfache Anpassung der Geschwindigkeit von Zug 1 im Verhältnis zu Zug 2. Führen Sie außerdem Ergebnisparameter im Modell ein, die die Wartezeiten beider Züge sowie ihre Summe messen.
Die Aufgabe besteht nun darin, einen Wert für den Faktor g zu ermitteln, für den die Summe der Wartezeiten der Züge minimal wird. Anstelle von manuellem Probieren lässt sich dafür die experiment-Funktion von TimeNET nutzen. Variieren Sie g im Bereich von 0.1 bis 4 und berechnen Sie die Ergebnisse mit TimeNET.
Die Ergebnisse (Werte der Ergebnisparameter für die verschiedenen Werte von g liegen danach in der Datei modellname.EXPRESULTS. Erstellen Sie bitte eine grafische Darstellung, die sowohl die Einzel- als auch die Gesamtwartezeit gegenüber g darstellt. Dazu können Sie z.B. gnuplot benutzen.
Die Lösung der Aufgabe beinhaltet einen Ausdruck/PDF des Modells mit den an die Transitionen geschriebenen Schaltzeiten, die Definition der Ergebnisparameter und einen Plot der Kurven, sowie die Angabe des optimalen Verhältnisses der Zuggeschwindigkeiten.